道家奇门遁甲作为中国传统的预测学之一,历史悠久,深奥难懂。其内容涵盖了天文、地理、人事等多个方面的综合运用,广泛应用于生活中的决策、趋利避害、选时择日等场景。随着现代科技的发展,在线排盘平台的出现让更多人能够便捷地接触到这一深奥的学问。本文将全面解析道家奇门遁甲的在线排盘方式,探讨其背后的原理、使用方法及其在实际生活中的应用。
奇门遁甲的基本原理
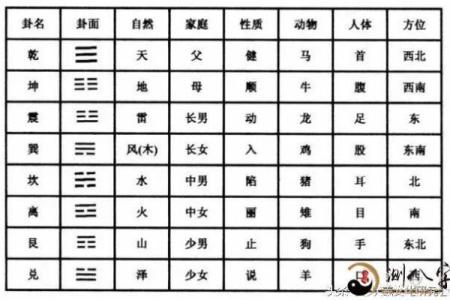
奇门遁甲是道家三式之一,与太极、八卦并列,属于先天之学。其核心思想基于阴阳五行的变化,结合天时、地利与人和,旨在通过一定的符号与运算推算出适合的时机和方位。奇门遁甲排盘的目的是通过对现有的时空环境进行分析,推测出某一事件的最佳发展路线。通过对天干地支、九宫八卦、神煞等因素的组合,奇门遁甲可以推算出某一时刻的吉凶祸福。
在实际排盘中,奇门遁甲的每一个盘面都是由“门、神、遁、星、宫、局”等多个元素组成。通过对这些元素的细致分析,可以得出关于某一事件或行动的全面预测。在线排盘则通过数字化的形式,将这一复杂的过程简化,利用现代算法快速生成预测结果,极大地方便了使用者。
如何在线排盘:流程与步骤
在线排盘的过程通常较为简便,用户只需要提供相关的出生日期和时间,系统便会自动生成奇门遁甲盘。首先,用户需要确认自己所处的时区和当地的时间,确保输入数据准确无误。接着,通过平台提供的排盘工具,系统会根据提供的时间和日期自动计算出与该时间点相关的奇门遁甲盘面,展示其中的门、神、星等数据。
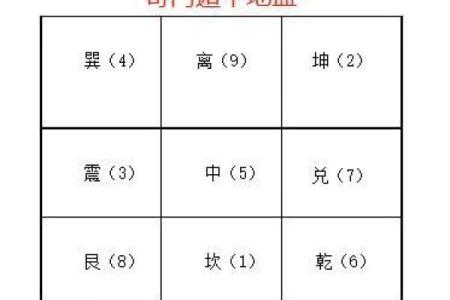
具体来说,奇门遁甲盘面包含了九宫格,每一个宫位代表不同的方位、时间段和能量场。在线排盘系统会根据输入的出生时间或其他特定时间点,确定哪些宫位受到吉星庇护,哪些则受到凶煞影响。同时,系统还会根据阴阳五行的相生相克关系,进一步分析宫位间的互动,预测不同事件的成败与时机。
奇门遁甲的应用场景
道家奇门遁甲的实际应用场景非常广泛,涵盖了个人决策、事业发展、婚姻家庭、健康管理等各个方面。无论是选择一个吉日进行重大活动,还是评估某个时机是否适合投资或创业,奇门遁甲都能提供有力的指导。
1. 择吉日与开运
通过奇门遁甲排盘,可以找到最适合进行重要活动的时机。例如,在选择结婚日期、开业日期或进行投资决策时,通过排盘查看各个时段的星宿和煞气,帮助你规避不利时段,选择吉祥的时机,从而提高成功率。
2. 个人命运分析
通过对个人八字与奇门遁甲的结合,能够进一步了解一个人的命运走向及其所面临的运势。比如,通过对某个人出生时的奇门遁甲盘进行分析,可以推测其一生的财运、事业运、婚姻运等方面的走势。这种分析帮助个人更好地把握自己的优势和劣势,做出更合理的生活和事业规划。

3. 事业决策与投资分析
在商业领域,奇门遁甲被广泛应用于市场分析、战略决策及投资时机的选择。例如,一家公司准备拓展新市场时,使用奇门遁甲来判断市场的潜力和时机,以确保决策的准确性与时效性。同时,通过排盘评估团队成员之间的合作关系,也能够更好地优化资源配置,提高团队整体效率。
4. 健康管理与防病祈安
奇门遁甲也能够在健康管理方面发挥一定的作用。通过排盘,可以预测某一时段可能对健康产生影响的因素,并采取相应的调整措施。通过对五行、宫位等的综合分析,判断某个时段是否适合进行治疗或手术,从而避免身体受到不利的影响。
奇门遁甲的优势与局限
道家奇门遁甲的优势在于其综合性和深刻的哲学底蕴。它不仅仅是一个简单的预测工具,更是与阴阳五行、天文学、地理学等领域相结合的系统。使用奇门遁甲进行排盘,不仅可以了解当前时局,还能帮助我们作出深思熟虑的决策。此外,奇门遁甲通过细致的时间和空间分析,能够准确预测特定事件的吉凶,提供科学的决策支持。
然而,奇门遁甲的局限性也不容忽视。首先,它需要依赖较为复杂的排盘方法和解盘技巧,对于初学者来说,理解和掌握其复杂的符号和理论是一个长期的过程。其次,尽管奇门遁甲能够提供一定的预测和建议,但它毕竟是一种概率性的学问,并不能保证每一次预测都百分之百准确。因此,在实际应用中,仍然需要结合个人的实际情况进行综合分析。
如何选择合适的在线排盘平台
随着奇门遁甲在线排盘的普及,市面上涌现了大量的排盘平台。选择一个靠谱的在线排盘平台,对于获得准确的结果至关重要。首先,用户应该选择那些界面清晰、操作简便的排盘工具,避免在使用过程中出现不必要的错误。其次,平台的排盘算法和分析工具是否准确,直接影响到最终的排盘结果。因此,用户可以根据平台的口碑和评价来选择最合适的服务。

值得注意的是,尽管在线排盘提供了便利,但对于深入分析和解读,建议还是寻求经验丰富的奇门遁甲师傅的帮助。这样可以避免在分析中出现偏差,确保预测的准确性和实用性。
道家奇门遁甲通过深奥的智慧和复杂的排盘系统,能够为我们的生活、工作以及决策提供有益的参考。在现代科技的加持下,在线排盘为我们打开了了解奇门遁甲的大门,帮助我们在复杂多变的环境中找到最有利的时机和路径。然而,无论技术如何发展,奇门遁甲的核心仍然是人的智慧与自然规律的结合,这也是其长期以来能够被人们推崇和应用的原因。